我们可以将直线 $y=10^5$ 和 V 形函数（下面称作三角形），逆时针旋转 $45°$，这样每进行一次操作，就相当于插入两条平行于 $x$ 轴和 $y$ 轴的直线，交点为三角形的顶点，记作 $(x, y)$。

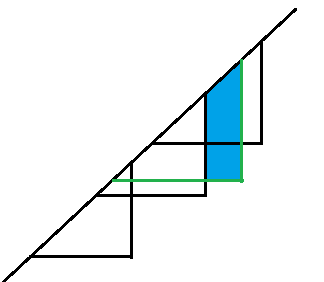
从图中可以看出，每当我们插入一个三角形，面积并就等于蓝色部分的面积加上左右两边的面积之和。蓝色部分的面积就是一个梯形的面积（也有可能是三角形，特判下即可），梯形右边界的长度可以通过三角形顶点的信息 $(x, y)$ 算出来。

此时我们需要计算梯形左边界对应的 $x$ 值，观察图形可以发现，产生左边界的原因是存在另一个三角形，它的下边界对应的 $y$ 比当前插入的三角形的下边界小，因此我们需要找到第一个小于当前三角形下边界的 $y$ 所对应的 $x$。

实现这一步操作的话，我们可以建一棵线段树，每次插入一个三角形，我们就在线段树的 $x$ 这个位置插入对应的 $y$ 值，然后维护区间最小值，查询的时候二分查找即可。

然后我们需要快速求出任意一段区间对应的面积，这一步也可以用线段树维护。每次插入一个三角形，需要改变的面积就是蓝色部分的面积，我们只需要记一下这个梯形的下边界的 $y$ 值，也就是进行区间推平操作，就可以把面积维护出来了。

我们可以将直线 $y=10^5$ 和 V 形函数（下面称作三角形），逆时针旋转 $45°$，这样每进行一次操作，就相当于插入两条平行于 $x$ 轴和 $y$ 轴的直线，交点为三角形的顶点。

我们需要维护的就是下方轮廓线，初始情况下是一条斜线。

从图中可以看出，每当我们插入一个三角形，轮廓线就有一部分需要区间推平。我们需要二分得到其推平左边界，然后对三角形进行区间推平。

线段树比较模板，就是写起来比较痛苦。

还有通过 set 维护轮廓的想法，但至今没人愿意写这个 std，感兴趣的可以尝试。

这里是代码